|
DOI: 10.7256/2454-0714.2017.4.24437
Дата направления статьи в редакцию:
15-10-2017
Дата публикации:
11-01-2018
Аннотация:
Предметом исследования является предложенная автором концепция иерархических bitmap-индексов. Она заключается в том, что в целях повышения производительности обработки запросов по фильтру времени индексы поддерживаются не только для значений основной единицы времени, но и произвольных более крупных кратных единиц. Объектом исследования является построение аналитической вероятностной модели таких индексов для частного случая экспоненциального распределения случайного потока занесения записей в базу данных. Автор уделяет основное внимание такому аспекту как вычисление дискретного распределения количества индексов, участвующих в обработке запроса. Методологией исследования являются теория вероятностей, методы комбинаторики, теория меры, вычислительный эксперимент. Кроме того, показано, что для исследования особенностей предложенной модели могут быть использованы новейшие понятия теории клеточных автоматов, такие как окрестность Зайцева. Основные результаты работы можно сформулировать следующим образом: введена оригинальная, интуитивно понятная концепция построения индексов; сформулированы новые, содержательные задачи оптимизации для выбора системы иерархических индексов; построена и верифицирована математическая модель, позволяющая оценить эффективность использования выбранной иерархии индексов. Показано, что в предельном случае модель естественным образом стремится к множеству фрактальной природы, в частности, одной из разновидностей канторовой пыли, для которой выведена формула вычисления ее размерности Хаусдорфа-Безиковича через прикладные параметры исходной задачи.
Ключевые слова:
иерархические bitmap-индексы, случайный поток событий, экспоненциальное распределение, полная вероятность, фрактальное множество, Канторова пыль, размерность Хаусдорфа-Безиковича, дизъюнкция, исключающее ИЛИ, окрестность Зайцева
Abstract: The subject of the study is the concept of hierarchical bitmap-indexes proposed by the author. It is that in order to improve the processing performance of queries on the time filter, the indices are supported not only for the values of the basic unit of time, but also for arbitrary larger multiple units. The object of the study is the construction of an analytic probability model of such indices for the particular case of the exponential distribution of a random stream of recording records in a database. The author focuses on such an aspect as the calculation of the discrete distribution of the number of indices involved in the processing of the query. The methodology of the study is probability theory, combinatorial methods, measure theory, computational experiment. In addition, it is shown that the latest concepts of the theory of cellular automata, such as the Zaitsev's neighborhood, can be used to study the features of the proposed model. The main results of the work can be formulated as follows: introduced an original, intuitive concept of building indexes; new, meaningful optimization problems for selecting a hierarchical index system are formulated; a mathematical model is constructed and verified, allowing to estimate the efficiency of using the chosen hierarchy of indices. It is shown that in the limiting case the model naturally tends to a set of fractal nature, in particular, one of the varieties of Cantor dust, for which the formula for calculating its Hausdorff-Besicovitch dimension is derived through the application parameters of the initial problem.
Keywords: hierarchical bitmap-indexes, random flow of events, exponential distribution, total probability, fractal set, Cantor dust, Hausdorff-Besikovitch dimensionality, disjunction, exclusive OR, Zaitsev's neighborhood
Введение
В работах [7,8] была предложена и исследована вероятностная модель для расчета распределения количества bitmap-индексов (далее просто – индексов), необходимых для выполнения запроса к базе данных. Кратко напомним постановку исходной задачи, следуя [7]. Предположим, что занесение новых записей в таблицу базы данных образует поток событий в непрерывном времени, описываемый стационарным случайным процессом с функцией распределения случайной величины 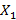 интервала между двумя последовательными событиями интервала между двумя последовательными событиями 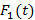 , а длина временнОго интервала, задаваемого в запросе на выборку записей, является случайной величиной , а длина временнОго интервала, задаваемого в запросе на выборку записей, является случайной величиной 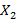 с распределением с распределением 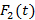 . Шкала времени разбита на равные интервалы единичной длины. Предположим также для определенности, что начало интервала для . Шкала времени разбита на равные интервалы единичной длины. Предположим также для определенности, что начало интервала для 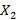 всегда совмещено с началом одного из единичных интервалов времени. Назовем полуоткрытый единичный интервал всегда совмещено с началом одного из единичных интервалов времени. Назовем полуоткрытый единичный интервал 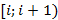 помеченным, если он содержит хотя бы одно событие из потока помеченным, если он содержит хотя бы одно событие из потока 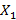 . Дискретную случайную величину Y определим как количество помеченных интервалов полностью накрываемых на временнОй шкале случайным интервалом . Дискретную случайную величину Y определим как количество помеченных интервалов полностью накрываемых на временнОй шкале случайным интервалом 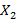 . Y является количеством индексов (дизъюнкций), используемых для вычисления результата запроса. Чем меньше эта величина, тем меньше времени занимает обработка запроса. . Y является количеством индексов (дизъюнкций), используемых для вычисления результата запроса. Чем меньше эта величина, тем меньше времени занимает обработка запроса.
Концептуальная идея настоящей работы заключается в следующем: количество индексов, необходимых для получения результата запроса, можно уменьшить, если наряду с мелким индексом, соответствующим основной единице времени (секунде), СУБД будет поддерживать еще некоторое количество крупных индексов, соответствующих интервалам времени, кратным основному. Например, если наряду с посекундными индексами мы располагаем также и поминутными, то для обслуживания запроса длиной в минуту (если его левая граница совпадает с границей минуты), нам понадобится максимум одна индексная битовая строка, а не 60. Идея проста и понятна, но ее использование, так же, как и всякой новой идеи, требует научного обоснования и методики расчета показателей ее эффективности. В частности, необходимо с той или иной точностью суметь дать ответ на следующие вопросы:
· как вычислить распределение случайной величины Y для заданной иерархии крупных индексов?
· как выбрать наиболее эффективную иерархию индексов и какие критерии эффективности использовать?
Иными словами, необходимо сформулировать и решить задачу анализа и далее – на ее основе - задачу синтеза. Как будет показано, каждая из этих задач является достаточно масштабной и комплексной, требует привлечения разнообразных средств математического моделирования. Настоящая работа является первым шагом в этом направлении и построена следующим образом. В первой части введены необходимые определения и обозначения, связанные с понятием иерархии индексов, сформулированы оригинальные задачи оптимизации для выбора иерархии. Во второй - основной части построена вероятностная модель, позволяющая для экспоненциального 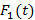 в совокупности с другими упрощающими предположениями получить распределение для Y, а, следовательно, и для математического ожидания этой величины. В третьей части установлена наглядная связь предельного случая модели иерархии индексов с разновидностью фрактального множества – канторовой пылью и выведена формула для фрактальной размерности этого множества в зависимости от прикладных параметров модели. Четвертая часть посвящена примерам численных расчетов на основе построенной модели, их графическому представлению и объяснению принципиальных особенностей результатов, в частности, на конкретных цифрах показано преимущество иерархии индексов по сравнению с использованием одного мелкого индекса. В заключении подведены краткие итоги работы и перечислены направления ближайших исследований. в совокупности с другими упрощающими предположениями получить распределение для Y, а, следовательно, и для математического ожидания этой величины. В третьей части установлена наглядная связь предельного случая модели иерархии индексов с разновидностью фрактального множества – канторовой пылью и выведена формула для фрактальной размерности этого множества в зависимости от прикладных параметров модели. Четвертая часть посвящена примерам численных расчетов на основе построенной модели, их графическому представлению и объяснению принципиальных особенностей результатов, в частности, на конкретных цифрах показано преимущество иерархии индексов по сравнению с использованием одного мелкого индекса. В заключении подведены краткие итоги работы и перечислены направления ближайших исследований.
1. Определения и формулировки
Введем понятие иерархии индексов как упорядоченного множества 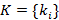 , i=1,..,N, где каждый элемент множества является натуральным числом больше единицы. Смысл этого понятия заключается в следующем: наряду с мелким индексом поддерживаются N крупных индексов, кратность первого по отношению к мелкому равна , i=1,..,N, где каждый элемент множества является натуральным числом больше единицы. Смысл этого понятия заключается в следующем: наряду с мелким индексом поддерживаются N крупных индексов, кратность первого по отношению к мелкому равна 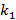 , кратность второго по отношению к первому равна , кратность второго по отношению к первому равна 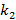 и т.д. N назовем размером иерархии. Например, K={60,60 } соответствует совокупности трех индексов размерами одна секунда, одна минута и один час. и т.д. N назовем размером иерархии. Например, K={60,60 } соответствует совокупности трех индексов размерами одна секунда, одна минута и один час.
Введем также множество 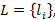 i=0,…,N, где i=0,…,N, где 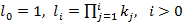 . Из определения понятно, что i-ый элемент этого множества есть размер i-го крупного индекса относительно основной единицы измерения – мелкого индекса. В данной работе мы будем рассматривать только такие интервалы времени, левая граница которых совпадает с границей самого крупного индекса, имеющего в иерархии K порядковый номер, равный размеру иерархии N. В примере {60,60} это начало любого часа. Это предположение, которое назовем элементарным граничным условием (ЭГУ), позволяет любой интервал времени длины T представить единственным образом в виде упорядоченного множества . Из определения понятно, что i-ый элемент этого множества есть размер i-го крупного индекса относительно основной единицы измерения – мелкого индекса. В данной работе мы будем рассматривать только такие интервалы времени, левая граница которых совпадает с границей самого крупного индекса, имеющего в иерархии K порядковый номер, равный размеру иерархии N. В примере {60,60} это начало любого часа. Это предположение, которое назовем элементарным граничным условием (ЭГУ), позволяет любой интервал времени длины T представить единственным образом в виде упорядоченного множества 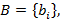 i=0,1,..,N, где i-ый элемент множества есть количество единиц i-го индекса иерархии, а i=0,1,..,N, где i-ый элемент множества есть количество единиц i-го индекса иерархии, а 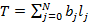 . Такое представление, как будет показано во второй части работы, позволяет построить вероятностную модель иерархии индексов, рассчитать ее и, в целом, «заглянуть» в особенности предложенной идеи. Интуитивно ЭГУ интерпретируется как своеобразная «нулевая» точка отсчета на временнОй шкале для интервала времени, заданного в запросе на выборку данных. В заключении работы будут предложены пути снятия данного ограничения. . Такое представление, как будет показано во второй части работы, позволяет построить вероятностную модель иерархии индексов, рассчитать ее и, в целом, «заглянуть» в особенности предложенной идеи. Интуитивно ЭГУ интерпретируется как своеобразная «нулевая» точка отсчета на временнОй шкале для интервала времени, заданного в запросе на выборку данных. В заключении работы будут предложены пути снятия данного ограничения.
Итак, любому запросу на выборку данных по времени при условии выполнения указанного ограничения соответствует некоторое множество B, представляющее разложение длины запроса по иерархии индексов. Установим важную связь между множествами B и K. Очевидно, что значение 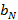 может быть произвольным неотрицательным целым числом, а для всех может быть произвольным неотрицательным целым числом, а для всех 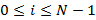 должно выполняться соотношение должно выполняться соотношение 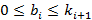 , т.к. количество индексов i-го уровня не может быть больше соответствующей ему кратности следующего уровня. Однако, такая интерпретация модели является не вполне экономичной. Верхнее ограничение можно уменьшить вдвое, если обратить внимание на следующее обстоятельство. Поясним его примером. Предположим, что имеются секундные и минутные индексы, и требуется построить выборку, где начало интервала времени совпадает с началом минуты, а длина интервала равна 45 секунд. Если вычислять результат запроса исключительно с помощью дизъюнкций, потребуется дизъюнкция 45 индексных битовых строк – от нулевой до 44-й секунды. Но их количество можно сократить до 16, если последовательно осуществить операцию «исключающее ИЛИ» полного минутного индекса с индексами от 45-й до 59-секунды. Иными словами, вместо «складывания» событий, произошедших от 0 до 44-й секунды, мы из всех событий, произошедших в течение минуты, «вычитаем» те события, которые в этот интервал не попали. Формализовав указанное соображение, запишем связь между множествами B и K в следующем виде, которым и будем пользоваться далее: , т.к. количество индексов i-го уровня не может быть больше соответствующей ему кратности следующего уровня. Однако, такая интерпретация модели является не вполне экономичной. Верхнее ограничение можно уменьшить вдвое, если обратить внимание на следующее обстоятельство. Поясним его примером. Предположим, что имеются секундные и минутные индексы, и требуется построить выборку, где начало интервала времени совпадает с началом минуты, а длина интервала равна 45 секунд. Если вычислять результат запроса исключительно с помощью дизъюнкций, потребуется дизъюнкция 45 индексных битовых строк – от нулевой до 44-й секунды. Но их количество можно сократить до 16, если последовательно осуществить операцию «исключающее ИЛИ» полного минутного индекса с индексами от 45-й до 59-секунды. Иными словами, вместо «складывания» событий, произошедших от 0 до 44-й секунды, мы из всех событий, произошедших в течение минуты, «вычитаем» те события, которые в этот интервал не попали. Формализовав указанное соображение, запишем связь между множествами B и K в следующем виде, которым и будем пользоваться далее:
|
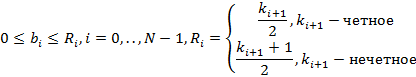
|
(1)
|
Отметим, что само понятие иерархического индексирования данных не является абсолютно новым и ранее вводилось и использовалось в моделях обработки потоков данных [9], но прикладная задача в этой работе решалась совершенно иная и была связана с динамическим анализом входных данных (data mining).
Интуитивно очевиден тот факт, что чем больше размер иерархии N, тем меньше будет значение 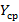 , т.е. тем меньше в среднем потребуется использовать битовых индексных строк для обслуживания запроса. Но, с другой стороны, поддержание лишнего крупного индекса требует определенных накладных расходов от СУБД, т.к. этот индекс нужно обновлять при каждой операции добавления и удаления записей, кроме того, требуется место, чтобы его хранить. Поэтому вполне естественно, что на размер иерархии должны накладываться некоторые ограничения. Это позволяет поставить содержательные проблемы условной оптимизации по выбору наилучшей в некоторой смысле иерархии K. , т.е. тем меньше в среднем потребуется использовать битовых индексных строк для обслуживания запроса. Но, с другой стороны, поддержание лишнего крупного индекса требует определенных накладных расходов от СУБД, т.к. этот индекс нужно обновлять при каждой операции добавления и удаления записей, кроме того, требуется место, чтобы его хранить. Поэтому вполне естественно, что на размер иерархии должны накладываться некоторые ограничения. Это позволяет поставить содержательные проблемы условной оптимизации по выбору наилучшей в некоторой смысле иерархии K.
Перед тем как сформулировать их, введем понятие веса иерархии 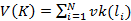 , где vk(x) – некоторая функция, отражающая зависимость накладных расходов на сопровождение крупного индекса от размера соответствующего ему интервала времени. Понятно, что эта функция является монотонно убывающей, т.к. чем крупнее индекс, тем меньше его значений приходится хранить и поддерживать. , где vk(x) – некоторая функция, отражающая зависимость накладных расходов на сопровождение крупного индекса от размера соответствующего ему интервала времени. Понятно, что эта функция является монотонно убывающей, т.к. чем крупнее индекс, тем меньше его значений приходится хранить и поддерживать.
Проблема 1. При заданном ограничении на вес иерархии 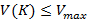 найти такую иерархию найти такую иерархию 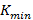 , которая минимизирует величину , которая минимизирует величину 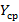 . .
Проблема 2. При заданном ограничении на величину 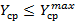 найти такую иерархию найти такую иерархию 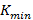 , которая минимизирует вес V(K). , которая минимизирует вес V(K).
Содержательность поставленных проблем оптимизации следует из того простого соображения, что увеличение размера иерархии N приводит к снижению 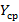 и к увеличению веса V(K). Однако, при простоте и ясности формулировок, решение любой из них наталкивается на серьезные сложности и требует решения двух принципиальных задач: и к увеличению веса V(K). Однако, при простоте и ясности формулировок, решение любой из них наталкивается на серьезные сложности и требует решения двух принципиальных задач:
Задача 1. Движок оптимизации - вычисление значения минимизируемой функции в заданной точке. В самом деле, как для заданной иерархии K вычислить значение 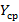 , которое обеспечивает эта иерархия? , которое обеспечивает эта иерархия?
Задача 2. Алгоритм оптимизации. Какой известный в теории или эвристический алгоритм оптимизации следует применить в нашем случае, когда носителем возможных решений выступает столь специфическое множество как описанное выше множество иерархий индексов?
Разумеется, дать исчерпывающие решения обеих задач в рамках одной статьи не представляется возможным. В настоящей работе будет сделан первый, но важный шаг – рассмотрено решение первой задачи в предположении ЭГУ и экспоненциального распределения для 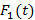 . .
2. Вероятностная модель
Сформулируем следующую задачу: для 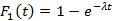 , произвольного распределения , произвольного распределения 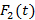 , заданной иерархии индексов , заданной иерархии индексов 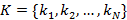 и в предположении удовлетворения всех запросов ЭГУ найти вероятность и в предположении удовлетворения всех запросов ЭГУ найти вероятность 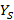 , S=0,1,2,… того, что поисковый запрос на выборку данных потребует использования ровно S индексов, каждый из которых может относиться к любому уровню иерархии. Понятно, что решение этой задачи дает распределение для случайной величины Y, а значит и искомую величину , S=0,1,2,… того, что поисковый запрос на выборку данных потребует использования ровно S индексов, каждый из которых может относиться к любому уровню иерархии. Понятно, что решение этой задачи дает распределение для случайной величины Y, а значит и искомую величину 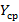 . Эта задача была решена в [7] для частного случая N=1 и . Эта задача была решена в [7] для частного случая N=1 и 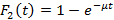 , где была выведена формула , где была выведена формула
|
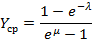
|
(2)
|
Эту формулу мы будем использовать как эталонную для оценки эффективности использования иерархии индексов по сравнению с единственным мелким индексом.
Определение. Назовем множество 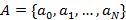 K-разложением числа S, если оно удовлетворяет совокупности следующих условий: K-разложением числа S, если оно удовлетворяет совокупности следующих условий:
· 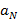 – произвольное неотрицательное целое число; – произвольное неотрицательное целое число;
· 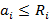 , i=0,..,N-1, где значения , i=0,..,N-1, где значения 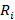 вычисляются по формуле (1); вычисляются по формуле (1);
· 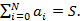
Нетрудно видеть, что событие, вероятность которого мы ищем, раскладывается на множество подсобытий, каждое из которых соответствует одному из возможных K-разложений S. Уже понятно, что смысл множества A состоит в том, что из S индексов, попадающих в фильтр запроса, 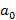 относятся к мелкому индексу, относятся к мелкому индексу, 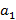 – к первому крупному индексу и т.д. При этом сделаем уточнение: использование для исключающего ИЛИ следующего по иерархии крупного индекса будем рассматривать как вклад в значение – к первому крупному индексу и т.д. При этом сделаем уточнение: использование для исключающего ИЛИ следующего по иерархии крупного индекса будем рассматривать как вклад в значение 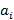 именно для предшествующего индекса. именно для предшествующего индекса.
Таким образом, поставленную задачу можно свести к следующей: найти вероятность того, что для удовлетворения запроса будет использовано заданное K-разложение. Тогда, если обозначить 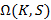 всё множество K-разложений S, искомую вероятность можно выразить как всё множество K-разложений S, искомую вероятность можно выразить как
|
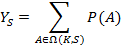
|
(3)
|
С понятием K-разложения тесно связана необходимость выполнения ЭГУ. Оно обеспечивает взаимную однозначность между длиной интервала времени и максимальным количеством индексов на каждом уровне иерархии для вычисления запроса по нему, что крайне важно при построении модели. Приведем простой пример. Пусть мелкий индекс – это секунда и имеется один крупный индекс для минут. Тогда для выполнения запроса на интервале длиной 61 секунд при выполнении ЭГУ максимальное значение S будет равно 12 с разложением {1,1}. С другой стороны, для иерархии {60} при выполнении ЭГУ по разложению {1,1} однозначно вычисляется длина интервала времени – 61. Теперь предположим, что выполнение ЭГУ необязательно. В этом случае интервалу с началом (n минут 5 секунд) и концом (n+1 минут 6 секунд) той же длины 61 будет соответствовать разложение {11,1}. В самом деле, для вычисления запроса нам понадобится 1 минутный индекс, его исключающее ИЛИ с первыми пятью секундными индексами и дизъюнкция шести секундных индексов следующей минуты.
Таким образом, разложению {11,1} при необязательности выполнения ЭГУ могут соответствовать как минимум две длины интервала – 61 и 71 (на самом деле – больше).
Возникает вопрос об оценке количества K-разложений, т.е. о количестве элементов множества 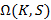 . Докажем следующее . Докажем следующее
Утверждение. Количество K-разложений числа S оценивается
|
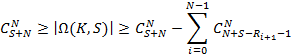
|
(4)
|
где N – размер иерархии.
Доказательство. Если бы не было ограничений 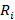 на количество используемых индексов всех уровней, кроме последнего, искомое значение было бы равно количеству разложений числа S на N+1 слагаемое, среди которых может быть произвольное число нулевых. Для этой задачи есть хорошо известное решение [1]: на количество используемых индексов всех уровней, кроме последнего, искомое значение было бы равно количеству разложений числа S на N+1 слагаемое, среди которых может быть произвольное число нулевых. Для этой задачи есть хорошо известное решение [1]: 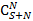 . Но ограничения существуют, поэтому из этой величины нам нужно исключить лишние разложения. Зафиксируем некий индекс i от 0 до N-1. Нам необходимо исключить те разложения, для которых значение . Но ограничения существуют, поэтому из этой величины нам нужно исключить лишние разложения. Зафиксируем некий индекс i от 0 до N-1. Нам необходимо исключить те разложения, для которых значение 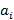 превышает превышает 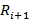 . Сколько же будет таких разложений? Для произвольного значения . Сколько же будет таких разложений? Для произвольного значения 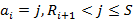 количество «лишних» разложений можно рассчитать как количество произвольных разложений числа S-j на N слагаемых, т.е. применить формулу из [1]. Просуммировав по всем j, получим количество «лишних» разложений можно рассчитать как количество произвольных разложений числа S-j на N слагаемых, т.е. применить формулу из [1]. Просуммировав по всем j, получим 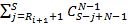 . Сделав замену z=S-j, приведем сумму к виду . Сделав замену z=S-j, приведем сумму к виду 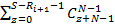 . В [3] приведена формула суммирования: . В [3] приведена формула суммирования: 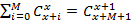 . Согласно ей, последняя сумма равна . Согласно ей, последняя сумма равна 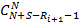 . Просуммировав по всем возможных позициям слагаемых, получим правую часть (4). Речь идет именно об ограничении снизу, а не о точном равенстве, поскольку разложения, для которых ограничения не выполняются более чем по одному индексу, буду исключаться согласно логике вывода (4), более одного раза. . Просуммировав по всем возможных позициям слагаемых, получим правую часть (4). Речь идет именно об ограничении снизу, а не о точном равенстве, поскольку разложения, для которых ограничения не выполняются более чем по одному индексу, буду исключаться согласно логике вывода (4), более одного раза.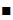
Алгоритмически множество 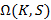 легко генерируется с помощью простой рекурсивной функции, реализацию на языке С которой приведем здесь с комментариями: легко генерируется с помощью простой рекурсивной функции, реализацию на языке С которой приведем здесь с комментариями:
rec(S,N+1); /*генерация разложения S на N+1 слагаемых с ограничениями*/
void rec(int sum, int n)
{
if (n==1) {
current[N]=sum;
print(current,out); /*вывод очередного разложения, представленного массивом current*/
return;
}
int s1=0;
for(int i=0;i<N+1-n;i++) s1+=current[i]; /*вычислили текущую уже накопленную сумму*/
s1=S-s1; /*сколько осталось до достижения S*/
inttop; /*верхнее ограничение для очередного слагаемого*/
if (s1<R[N+1-n]) top=s1; /*сравниваем с заданным ограничением*/
else top=R[N+1-n];
for(int i=0;i<=top;i++) {
current[N+1-n]=i; /*зафиксировали очередное слагаемое*/
rec(s-i,n-1); /*рекурсивный вызов: то, что осталось, разбиваем на n-1 слагаемых*/
}
}
Вернемся теперь к задаче вычисления P(A), т.е. вероятности заданного разложения 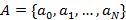 . .
Определение. Множество 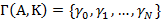 назовем носителем разложения A в иерархии K, если его элементы удовлетворяют следующим условиям: назовем носителем разложения A в иерархии K, если его элементы удовлетворяют следующим условиям:
1) 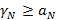 ; ;
2) 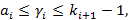 i=0,..,N-1, i=0,..,N-1, 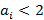 ; ;
3) 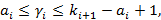 i=0,..,N-1, i=0,..,N-1, 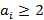 . .
На введенном только что понятии носителя остановимся подробнее, т.к. оно является ключевым связующим понятием между прикладной логикой задачи и ее формализацией в математической модели. Смысл его заключается в том, что множество носителей описывает в виде их представления в K-иерархии все возможные длины интервалов времени, заданные в фильтре запроса, для которых набор индексов, используемых для вычисления результата запроса, может быть представлен разложением A. Чтобы быстро и наглядно представить суть вопроса, вновь рассмотрим иерархию K={60} – индексы для секунд и минут, 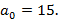 При При 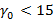 значение 15 для значение 15 для 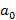 никак не может быть достигнуто, даже если будут непустыми все никак не может быть достигнуто, даже если будут непустыми все 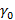 мелких индексов – их просто не хватит. При значении мелких индексов – их просто не хватит. При значении 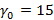 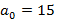 будет достигнуто, если будут непустыми все первые 15 мелких индексов – от значения 0 до значения 14; при значении будет достигнуто, если будут непустыми все первые 15 мелких индексов – от значения 0 до значения 14; при значении 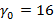 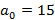 получается, если из первых шестнадцати мелких индексов будет 15 заполненных и один пустой, т.е. для 15 секундных интервалов из 16 есть хотя бы одна запись, а для одного интервала ни одной записи нет. Эту логику можно продолжать до значения получается, если из первых шестнадцати мелких индексов будет 15 заполненных и один пустой, т.е. для 15 секундных интервалов из 16 есть хотя бы одна запись, а для одного интервала ни одной записи нет. Эту логику можно продолжать до значения 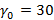 , для значения же 31 логика изменится. В этом случае , для значения же 31 логика изменится. В этом случае 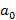 будет равно 15, если: а) минутный крупный индекс является непустым; б) из 29 мелких индексов, соответствующих секундам с 31 по 59 14 индексов являются непустыми, а 15 пусты (минутный крупный индекс, используемый для вычисления исключающего ИЛИ, идет в счет будет равно 15, если: а) минутный крупный индекс является непустым; б) из 29 мелких индексов, соответствующих секундам с 31 по 59 14 индексов являются непустыми, а 15 пусты (минутный крупный индекс, используемый для вычисления исключающего ИЛИ, идет в счет 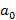 в силу уточнения, сделанного после определения K-разложения). Максимальное значение в силу уточнения, сделанного после определения K-разложения). Максимальное значение 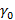 , для которого работает эта логика – 46. В самом деле, в этом случае 15 достигается при непустом минутном и всех 14 секундных индексах от 46 до 59. При , для которого работает эта логика – 46. В самом деле, в этом случае 15 достигается при непустом минутном и всех 14 секундных индексах от 46 до 59. При 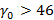 оставшихся индексов уже не хватит, даже если все они будут непустыми. Мы проиллюстрировали условие 3 из определения носителя. оставшихся индексов уже не хватит, даже если все они будут непустыми. Мы проиллюстрировали условие 3 из определения носителя.
Теперь пусть 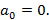 В этом случае В этом случае 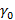 может принимать любое значение от 0 до 59 при условии, что минутный индекс пуст (это условие, как и все прочие, будет отражено при записи вероятностных уравнений). Если же может принимать любое значение от 0 до 59 при условии, что минутный индекс пуст (это условие, как и все прочие, будет отражено при записи вероятностных уравнений). Если же 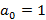 , максимальное значение , максимальное значение 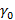 опять-таки равно 59. При этом опять-таки равно 59. При этом 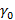 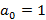 будет достигнуто при непустом минутном индексе (который и станет тем единственным) и пустом мелком индексе для значения 59. будет достигнуто при непустом минутном индексе (который и станет тем единственным) и пустом мелком индексе для значения 59.
Таким образом, мы готовы к тому, чтобы выписать формулу для P(A). В силу свойства отсутствия последействия у экспоненциального распределения (и только у него) она имеет следующий мультипликативный вид:
|
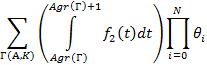
|
(5)
|
где:
- суммирование ведется по всем носителям;
-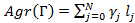 – длина интервала времени для данного носителя; – длина интервала времени для данного носителя;
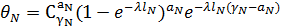
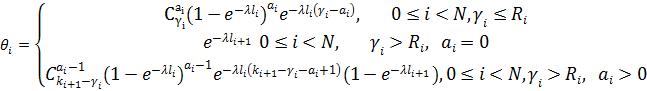
Форма записи формулы (5) является математически корректной, но для программной реализации она не слишком удобна, т.к. не вполне понятно, как перебирать носители во внешней сумме. Запишем (5) в другом виде, быть может, более громоздком и менее формальном, но зато использующем определение носителя и поэтому удобном для реализации:
|
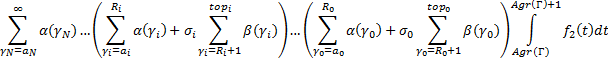
|
(6)
|
где:
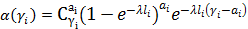
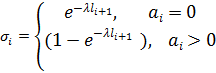
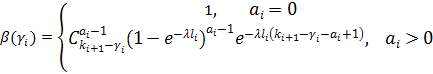
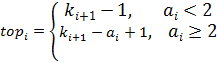
Смысл записи (6) состоит в том, что если раскрыть все скобки и перемножить «всё со всем», получим как и в (5) сумму всех цепочек произведений носителей с интегралом в конце каждой цепочки, который берется для аггрегированного значения каждой цепочки-носителя. Такая запись позволяет легко запрограммировать вычисление выражения (6) в виде рекурсивной функции, которая последовательно вызывает сама себя от уровня N до уровня 0, передавая три аргумента: номер уровня, накопленное на данном уровне значение произведения и накопленное на данном уровне агрегированное значение носителя. На уровне 0 происходит домножение на значение интеграла и наращивание глобального значения итоговой суммы произведением очередной завершенной цепочки-носителя. Рекурсивные вызовы производятся в цикле по всем значениям 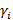 на i-ом уровне. на i-ом уровне.
Верифицировать построенную модель можно, если учесть, что сумма всех вероятностей 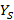 , вычисленных по формуле (3), по S от нуля до бесконечности, должна сходиться к единице, т.к. образует полную группу событий. Такую проверку можно выполнить: , вычисленных по формуле (3), по S от нуля до бесконечности, должна сходиться к единице, т.к. образует полную группу событий. Такую проверку можно выполнить:
· экспериментально. Данная проверка, выполненная для широкого диапазона входных данных, показала по результатам расчетов сходимость ряда к единице с высокой точностью. Более подробно численные результаты анализируются в четвертом разделе;
· теоретически. Можно доказать, что ряд из (3), составленный из всевозможных вероятностей, вычисленных по формуле (6), сходится к единице. Из-за обилия и громоздкости выкладок нет необходимости утомлять этим доказательством читателя в рамках данной статьи. Опишем лишь его основную идею. Для каждого целочисленного значения j группируются все слагаемые, содержащие множитель 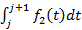 , и доказывается, что их сумма равна единице (сумма получается полной разверткой бинома Ньютона той или иной степени). В итоге получается , и доказывается, что их сумма равна единице (сумма получается полной разверткой бинома Ньютона той или иной степени). В итоге получается 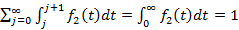 , т.к. , т.к. 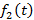 является плотностью распределения вероятностей. является плотностью распределения вероятностей.
3. Канторова пыль
Осмысление построенной модели и ее представления формулой (6) приводит к достаточному очевидному выводу о вложенности понятия носителя разложения A. Если зафиксировать интервал времени, соответствующий величине самого крупного N-го индекса и последовательно строить носитель, начиная с (N-1)-го индекса и опускаясь до самого мелкого, то нетрудно видеть, что каждое последующее приближение носителя лежит внутри предыдущего и является его частью. Возникает вопрос: что представляет собой носитель в пределе, если устремить значение размера иерархии N к бесконечности? Чтобы ответить на него, рассмотрим наиболее простой случай. Пусть иерархия представляет собой множество с одинаковыми элементами K={k,k,k,…k}, а разложение A={a,a,a,…a}, a<k/2. Примем длину интервала для самого крупного индекса за единицу и рассмотрим последовательное построение носителя внутри этого интервала. На первой итерации получим отрезок [a/k; (k-a+1)/k], который будем интерпретировать как k-2a+1 отрезков длиной 1/k каждый. Чтобы произвести вторую итерацию, 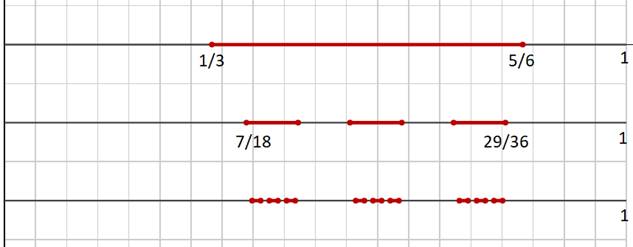
Рис.1. Три уровня для k=6, a=2.
необходимо каждый из этих отрезков разделить на k равных частей и взять внутри k-a+1 этих частей, отступив от начала отрезка aчастей. Получим 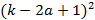 отрезков длиной отрезков длиной
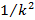 каждый. Аналогичные действия проводим на третьей итерации и т.д. Рисунок 1 иллюстрирует первые три итерации для k=6 и a=2. каждый. Аналогичные действия проводим на третьей итерации и т.д. Рисунок 1 иллюстрирует первые три итерации для k=6 и a=2.
Таким образом, на каждой итерации количество равных отрезков, составляющих носитель множества A, увеличивается в k-2a+1 раз, длина же каждого отрезка уменьшается в k раз. Нетрудно видеть, что в пределе мы получаем фрактальное множество [6] с размерностью Хаусдорфа-Безиковича
|
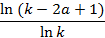
|
(7)
|
Данное множество является одной из многочисленных разновидностей наиболее известного и, пожалуй, самого первого фрактала – канторовой пыли, который подробно и всесторонне рассматривается, например, в [2],[4] и [5]. Анализируя (7), можно заметить, что фрактальная размерность построенного нами предельного носителя уменьшается с ростом a. Это логично, т.к. с ростом a диапазон изменения носителя согласно его определению уменьшается. Так, при k=60 и a=30 (максимальное значение) носитель состоит всего из двух значений – 30 и 31.
Комментируя полученный результат, можно отметить следующее. Теория фракталов возникла и приобрела большую популярность с конца 80-х годов прошлого столетия. С тех пор появилось большое количество публикаций (в том числе и на русском языке), в которых с использованием далеко развитого математического аппарата рассматривались те или иные математические аспекты этой теории, либо на основе простых итерационных формул строились удивительные по красоте изображения. Работы же, с той или иной степенью убедительности демонстрирующие прикладное значение фракталов, были достаточно редкими, во всяком случае, в области Computer Science, хотя подобного рода попытки неоднократно предпринимались. В частности, отметим в этом отношении [10] и [11]. Эти и другие работы построены, как правило, по следующей логической схеме. Рассматривается некий большой набор данных, полученный в результате логирования (выполнения отладочных печатей) работы какой-то сложной программной системы (например, компилятора или СУБД). Выдвигается гипотеза о фрактальных свойствах этих данных, затем методами математической статистики эта гипотеза в той или иной степени подтверждается, оценивается их фрактальная размерность, после чего делается вывод о перспективах прогностических возможностей по отношению к данным на основе их фрактальной модели. В нашем же случае классический фрактал возник естественным образом непосредственно из сути сугубо прикладной задачи в области Computer Science. Возник он ввиду того, что понятие носителя, на котором строится математическая модель иерархических индексов, обладает свойством вложенности и самоподобия на каждом уровне иерархии.
4. Численные результаты
Вычисления по формулам (3), (6) велись для экспоненциальных распределений 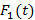 и и 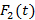 c c 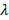 =1/30 и =1/30 и 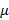 =0.001. Это соответствует появлению новой записи в БД примерно каждые 30 секунд и средней длине фильтра запроса 17 минут, т.е. ищутся все записи, занесенные в БД за период в среднем 17 минут. Сходимость внешнего ряда в (6) фиксировалась по достижении точности =0.001. Это соответствует появлению новой записи в БД примерно каждые 30 секунд и средней длине фильтра запроса 17 минут, т.е. ищутся все записи, занесенные в БД за период в среднем 17 минут. Сходимость внешнего ряда в (6) фиксировалась по достижении точности 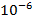 . Для каждого эксперимента проверялось выполнения условия . Для каждого эксперимента проверялось выполнения условия 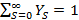 до достижения значения 0.999. Входящие в (6) величины, обозначенные символами α и β, вычислялись наиболее аккуратным образом, чтобы промежуточные значения были не слишком велики и не слишком малы. Приведем код их вычисления с комментариями. до достижения значения 0.999. Входящие в (6) величины, обозначенные символами α и β, вычислялись наиболее аккуратным образом, чтобы промежуточные значения были не слишком велики и не слишком малы. Приведем код их вычисления с комментариями.
/*a – верхнее число для количества сочетаний
b – нижнее число для количества сочетаний
x – значение экспоненты в соответствующей отрицательной степени*/
double comb(int a, int b,double x)
{
double res;
int big;
if (a>b-a) big=a;
else big=b-a; /*что больше – верхнее число или разность нижнего и верхнего?*/
res=1.0;
/*вычисляем сокращенное на все возможные общие множители число сочетаний, домножая по ходу вычислений на экспоненциальные множители*/
for (int i=0;i<b-big; i++) {
res=(res*(big+i+1)/(i+1))*(1-x)*x;
}
/*итераций в этом цикле не хватило для нужных степеней экспоненциальных сомножителей, поэтому домножаем то, что осталось*/
if (big==a) for(int i=0;i<2*a-b;i++) res=res*(1-x);
else for(int i=0;i<b-2*a;i++) res=res*x;
return(res);
}
При отсутствии иерархии значение 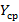 , рассчитанное по формуле (2), равно 32.4. На это значение далее будем ссылаться как на эталонное. , рассчитанное по формуле (2), равно 32.4. На это значение далее будем ссылаться как на эталонное.
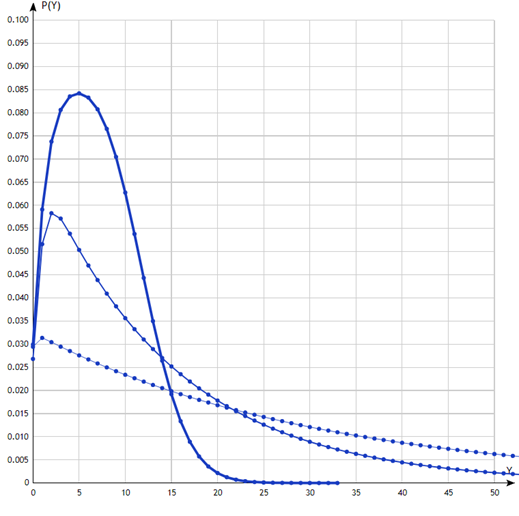
Рис. 2. K={600} – толстая линия, K={60} – средняя, K={6} - тонкая
На рис.2 изображены распределения случайной величины 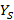 для размера иерархии N=1, K={6}, {60} и {600}. Мы видим, что наиболее медленно для размера иерархии N=1, K={6}, {60} и {600}. Мы видим, что наиболее медленно 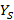 стремится к нулю для первой из этих иерархий. Это вполне закономерно, исходя из следующих рассуждений. Мы применяем в среднем 1000-секундные запросы, записи на протяжении этой тысячи секунд появляются примерно каждые 30 секунд. В этой ситуации 6-секундные индексы будут практически бесполезны, т.к. в каждом таком индексе будет содержаться в статистическом смысле только по одной записи, и для покрытия интервала запроса потребуется много таких индексов. стремится к нулю для первой из этих иерархий. Это вполне закономерно, исходя из следующих рассуждений. Мы применяем в среднем 1000-секундные запросы, записи на протяжении этой тысячи секунд появляются примерно каждые 30 секунд. В этой ситуации 6-секундные индексы будут практически бесполезны, т.к. в каждом таком индексе будет содержаться в статистическом смысле только по одной записи, и для покрытия интервала запроса потребуется много таких индексов.
На рис.3 показаны распределения  для N=2, K={6,600}, {60,60}, {600,6}. Т.е. в качестве самого крупного индекса во всех случаях используется часовой, в качестве первого – шестисекундный, минутный и десятиминутный. Принципиально картина та же, что и для N=1. для N=2, K={6,600}, {60,60}, {600,6}. Т.е. в качестве самого крупного индекса во всех случаях используется часовой, в качестве первого – шестисекундный, минутный и десятиминутный. Принципиально картина та же, что и для N=1.
Рис.3. K={600,6} – толстая линия, K={60,60} - средняя, K={6,600} – тонкая
На рис.4 приведены зависимости ключевой характеристики 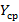 от k для N=1, K={k} и для N=2, K={k,3600/k}. Эти результаты представляют наибольший интерес, т.к. в какой-то мере подводят практический итог всей статье. Мы видим, что первая кривая действительно имеет ожидаемый минимум, достигаемый приблизительно на значении 345 (т.е. размер индекса – немногим менее 6 минут) и равный около 5.7. Оптимальное значение от k для N=1, K={k} и для N=2, K={k,3600/k}. Эти результаты представляют наибольший интерес, т.к. в какой-то мере подводят практический итог всей статье. Мы видим, что первая кривая действительно имеет ожидаемый минимум, достигаемый приблизительно на значении 345 (т.е. размер индекса – немногим менее 6 минут) и равный около 5.7. Оптимальное значение 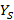 получилось примерно в 5.5 раз меньше эталонного, т.е. поставленные в работе проблемы являются достаточно перспективными. Далее отметим, что с ростом k индекс становится всё менее и менее полезным, в конце концов его наличие практически перестает ощущаться, и кривая асимптотически стремится к эталонному значению. Безусловно, существует некая эмпирическая зависимость между получилось примерно в 5.5 раз меньше эталонного, т.е. поставленные в работе проблемы являются достаточно перспективными. Далее отметим, что с ростом k индекс становится всё менее и менее полезным, в конце концов его наличие практически перестает ощущаться, и кривая асимптотически стремится к эталонному значению. Безусловно, существует некая эмпирическая зависимость между 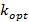 и значениями λ и μ, а, возможно, и вторыми моментами распределений и значениями λ и μ, а, возможно, и вторыми моментами распределений 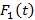 и и 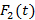 . Но вид этой зависимости пока что остается неизвестным и требует более детальных исследований. . Но вид этой зависимости пока что остается неизвестным и требует более детальных исследований.
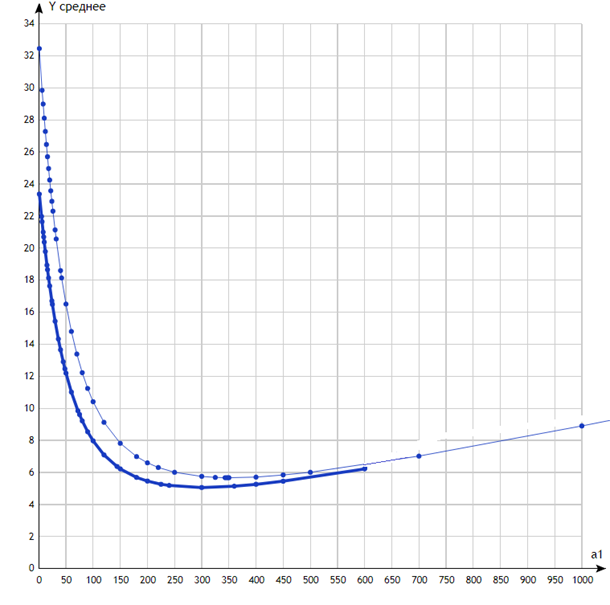
Рис. 4. N=1 – тонкая линия, N=2 – толстая
Что же касается кривой для N=2, то ее минимум достигается при достаточно близком к первому значении k=300 и равен приблизительно 5.06, т.е. незначительно, но лучше минимального значения для N=1. Однако, вопрос об оптимальном решении для всего множества иерархий N=2 остался открытым, т.к. в данном эксперименте мы искусственно сократили для N=2 количество переменных до одной – в общем случае требуется решение задачи 2.
Теперь вспомним о том факте, что модель требует экспоненциальности только от распределения 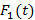 , распределение же , распределение же 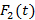 может быть произвольным. Поэтому описание численных экспериментов было бы неполным без наличия результата для какого-либо иного может быть произвольным. Поэтому описание численных экспериментов было бы неполным без наличия результата для какого-либо иного 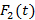 . Другое дело, что мы не будем иметь для сравнения эталонного значения, т.к. формула (2) была выведена в предположении экспоненциальности обоих распределений. На рис.5 приведена зависимость . Другое дело, что мы не будем иметь для сравнения эталонного значения, т.к. формула (2) была выведена в предположении экспоненциальности обоих распределений. На рис.5 приведена зависимость 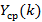 при N=1 для распределения Вейбулла: при N=1 для распределения Вейбулла:
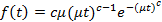
c=0.5, λ=1/30, μ=0.002. При данных параметрах сохраняется математическое ожидание, равное 1000, т.к. для распределения Вейбулла оно равно 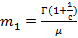 , где Γ(x) – гамма-функция. , где Γ(x) – гамма-функция.
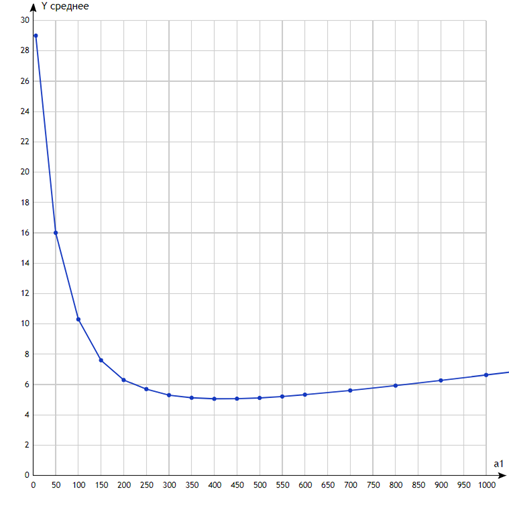
Рис. 5. Распределение Вейбулла, N=1
Минимальное значение 5.06 достигается при k≈400, и в целом после достижения минимума кривая растет медленнее, чем ее аналог для экспоненциального распределения. Такое поведение вполне можно объяснить, если принять во внимание различие в среднеквадратичном отклонении распределений при одном и том же математическом ожидании. Для экспоненциального оно совпадает с таковым и тоже равно 1000. Для распределения Вейбулла оно вычисляется по формуле
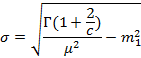
и в нашем случае равно 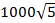 , т.е. в два с лишним раза больше. Следовательно, в первом случае верхней «границей кадра», в который попадают длины интервалов запросов, можно считать 1000+1000=2000, во втором же случае эта граница больше 3000. Поэтому крупный индекс одного и того же размера оказывается при распределении Вейбулла более «полезным», т.к. для него есть «работа», которой при экспоненциальном распределении нет. Этим же объясняется, что значение , т.е. в два с лишним раза больше. Следовательно, в первом случае верхней «границей кадра», в который попадают длины интервалов запросов, можно считать 1000+1000=2000, во втором же случае эта граница больше 3000. Поэтому крупный индекс одного и того же размера оказывается при распределении Вейбулла более «полезным», т.к. для него есть «работа», которой при экспоненциальном распределении нет. Этим же объясняется, что значение 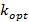 при прочих одинаковых параметрах для распределения Вейбулла несколько больше. при прочих одинаковых параметрах для распределения Вейбулла несколько больше.
В ходе экспериментального изучения особенностей распределения 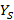 , рассчитанного с использованием построенной модели, можно поставить еще немало вопросов. Поскольку ключевую роль в этой модели играет формула (6) вычисления вероятности отдельно взятого разложения , рассчитанного с использованием построенной модели, можно поставить еще немало вопросов. Поскольку ключевую роль в этой модели играет формула (6) вычисления вероятности отдельно взятого разложения 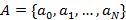 как сумма вероятностей по всем возможным носителям, интерес представляет вопрос о вкладе различных носителей в эту вероятность. Равномерно ли распределен этот вклад по всему множеству носителей, либо он зависит от определенной «близости» носителя к множеству A? Чтобы исследовать этот вопрос необходимо построить какую-либо метрику, количественно выражающую эту «близость». Говорить о метрике логично и уместно, так как и множество-разложение A и множество-носитель Γ представляют собой множества целых неотрицательных чисел одного и того же размера N. При построении такой метрики могут помочь новейшие идеи и понятия из смежных областей Computer Science, в частности теории клеточных автоматов. Одной из таких идей является окрестность Зайцева [12]. Используя эту плодотворную идею, можно дать следующее как сумма вероятностей по всем возможным носителям, интерес представляет вопрос о вкладе различных носителей в эту вероятность. Равномерно ли распределен этот вклад по всему множеству носителей, либо он зависит от определенной «близости» носителя к множеству A? Чтобы исследовать этот вопрос необходимо построить какую-либо метрику, количественно выражающую эту «близость». Говорить о метрике логично и уместно, так как и множество-разложение A и множество-носитель Γ представляют собой множества целых неотрицательных чисел одного и того же размера N. При построении такой метрики могут помочь новейшие идеи и понятия из смежных областей Computer Science, в частности теории клеточных автоматов. Одной из таких идей является окрестность Зайцева [12]. Используя эту плодотворную идею, можно дать следующее
Определение. m-окрестностью Зайцева разложения 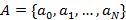 , (1≤m≤N), назовем такое множество носителей , (1≤m≤N), назовем такое множество носителей 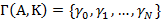 , для которого условие , для которого условие 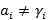 (0≤i≤N-1) выполнено ровно для m элементов из N. (0≤i≤N-1) выполнено ровно для m элементов из N.
Данное определение разбивает всё множество носителей на N непересекающихся подмножеств – m-окрестностей Зайцева и, соответственно, позволяет разбить и общую сумму (6) на N составляющих, вычисленных по этим подмножествам. Это даст возможность исследовать, насколько различаются составляющие для различных значений m, является ли эта зависимость монотонной или нет. Отметим, что строго говоря, существует и 0-окрестность множества A – это само множество A, которое тоже согласно определению является носителем. Но наличие только одного элемента делает эту окрестность малосодержательной.
Заключение
Построенная в работе модель позволила дать весьма привлекательные и обнадеживающие оценки эффективности использования иерархических индексов. Однако, наложенные при ее построении ограничения пока не позволяют говорить о том, что мы получили исчерпывающее решение хотя бы только задачи 1 – построения движка оптимизации. Этих ограничений два: пуассоновское свойство потока занесения новых записей в базу данных и выполнение элементарного граничного условия. По ходу построения модели уже отмечалось, что снятие любого из двух ограничений сразу же разрушает модель, при том что даже такая модель получилась достаточно сложной. Очевидно, что без наложения указанных ограничений построение аналитической модели является задачей неразрешимой. Поэтому следующим шагом в решении задачи должно стать построение имитационной модели, ее верификация на уже известном аналитическом решении и создание методики получения результатов на ее основе.
Относительно первого ограничения всё достаточно ясно – произвольное распределение моделируется соответствующим ему генератором случайных чисел. Снятие же второго ограничения уже не столь очевидно и требует дополнений к постановке задачи. Если допустить, что начало интервала времени, по которому происходит выборка записей, может приходиться на произвольный момент времени, то следует учесть тот реалистичный факт, что эти моменты отнюдь не равновероятны. Так, если ориентироваться на традиционную иерархию интервалов секунда-минута-час, вероятность начала интервала для момента времени, не кратного минуте, будет существенно ниже, чем для кратного. В то же время вероятность начала интервала для минут, не кратных 5, будет меньше, чем для кратных; кратных 5, но не кратных 15 – меньше, чем для кратных 15 и т.д. А для моментов, кратных часу тоже будет иная вероятность. Эти рассуждения показывают необходимость описать распределение или даже совокупность распределений вероятностей, позволяющих гибко описывать произвольность начальных точек интервалов запросов на временнОй шкале. В этой связи открытым остается вопрос, насколько ухудшится эффективность использования иерархических индексов, рассчитанная в данной работе, если рассчитывать ее при реалистичном условии той или иной произвольности начальных точек интервалов, сняв ЭГУ. Ответ на этот вопрос как раз и сможет дать только имитационная модель.
Благодарности
Автор выражает благодарность своему сыну, студенту факультета ВМК МГУ Михаилу Трубу за помощь, оказанную при подготовке графического материала и полезные советы при разработке программного обеспечения.
Библиография
1. Виленкин Н.Я. Комбинаторика.-М.: Наука, 1969.-328 с.
2. Герега А.Н. Конструктивные фракталы в теории множеств.-Одесса, "Освита Украины", 2017.-85 с.
3. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений.-СПб, БХВ, 2011, 7-е изд.-1232 с.
4. Деменюк С.Л. Фрактал: между мифом и ремеслом.-Академия исследования культуры РИНВОЛ, СПб, 2011.-296 с.
5. Кроновер Р.М. Фракталы и хаос в динамических системах.-Москва: Постмаркет, 2000.-352 с.
6. Мандельброт Б. Фрактальная геометрия природы.-Москва, Институт компьютерных исследований, 2002.-656 с.
7. Труб И.И. Аналитическое вероятностное моделирование bitmap-индексов //Программные системы и вычислительные методы.-2016-№ 4.-с.315-323. DOI: 10.7256/2305-6061.2016.4.2109
8. Труб И.И. О распределении количества bitmap-индексов для произвольного потока занесения записей в базу данных //Программные системы и вычислительные методы.-2017.-№ 1.-с.11-21. DOI: 10.7256/2454-0714.2017.1.21790
9. Bulut A., Singh A.K. Indexing and Querying Data Streams.-In book DataStreams: Models and Algorithms (edited by Charu C. Aggarwal).-Springer, 2007, 373 p.-pp.237-259.
10. McNutt B. The Fractal Structure of Data Reference: Application to the Memory Hierarchy. - Kluwer Academic, Boston, 2000. - 132 p.
11. Thiebaut D. From the fractal dimension of the intermiss gaps to the cache-miss ratio. - IBM J. Res. Develop., vol.32, No. 6, November, 1988. - pp.796-803.
12. Zaitsev D. A generalized neighborhood for cellular automata.-Theoretical Computer Science, 666 (2017), pp. 21-35
References
1. Vilenkin N.Ya. Kombinatorika.-M.: Nauka, 1969.-328 s.
2. Gerega A.N. Konstruktivnye fraktaly v teorii mnozhestv.-Odessa, "Osvita Ukrainy", 2017.-85 s.
3. Gradshtein I.S., Ryzhik I.M. Tablitsy integralov, summ, ryadov i proizvedenii.-SPb, BKhV, 2011, 7-e izd.-1232 s.
4. Demenyuk S.L. Fraktal: mezhdu mifom i remeslom.-Akademiya issledovaniya kul'tury RINVOL, SPb, 2011.-296 s.
5. Kronover R.M. Fraktaly i khaos v dinamicheskikh sistemakh.-Moskva: Postmarket, 2000.-352 s.
6. Mandel'brot B. Fraktal'naya geometriya prirody.-Moskva, Institut komp'yuternykh issledovanii, 2002.-656 s.
7. Trub I.I. Analiticheskoe veroyatnostnoe modelirovanie bitmap-indeksov //Programmnye sistemy i vychislitel'nye metody.-2016-№ 4.-s.315-323. DOI: 10.7256/2305-6061.2016.4.2109
8. Trub I.I. O raspredelenii kolichestva bitmap-indeksov dlya proizvol'nogo potoka zaneseniya zapisei v bazu dannykh //Programmnye sistemy i vychislitel'nye metody.-2017.-№ 1.-s.11-21. DOI: 10.7256/2454-0714.2017.1.21790
9. Bulut A., Singh A.K. Indexing and Querying Data Streams.-In book DataStreams: Models and Algorithms (edited by Charu C. Aggarwal).-Springer, 2007, 373 p.-pp.237-259.
10. McNutt B. The Fractal Structure of Data Reference: Application to the Memory Hierarchy. - Kluwer Academic, Boston, 2000. - 132 p.
11. Thiebaut D. From the fractal dimension of the intermiss gaps to the cache-miss ratio. - IBM J. Res. Develop., vol.32, No. 6, November, 1988. - pp.796-803.
12. Zaitsev D. A generalized neighborhood for cellular automata.-Theoretical Computer Science, 666 (2017), pp. 21-35
|


















 Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
 Рус
Рус



